In machine learning, a loss function is used to measure the loss, or cost, of a specific machine learning model. These loss functions calculate the amount of error in a specific machine learning model using some mathematical formula and measure the performance of that specific model.

There are various loss functions that are used in machine learning for regression and classification problems. In the process of the machine learning model building, our aim is to minimize the loss/cost function and therefore increase the accuracy of the model.

In this article, we will go through various loss functions used in machine learning models for regression and classification problems. Let’s get started!

Loss functions for Regression

Mean Squared Error

The mean squared error (MSE) measures the amount of error in machine learning regression models by calculating the average squared distance between the observed and predicted values in our data.

This loss function penalizes the model for large errors by squaring them and therefore making the model less robust to the outliers. We should not use this loss function when the dataset is prone to too many outliers.

For a good model/estimator, the value of the MSE should be closer to zero.

If we have a data point Yi and the predicted value for this point is Ŷi, then the mean squared error can be calculated as:

Where n is the total number of observations in our dataset.

Example:

import numpy as npdef mean_squared_error(true_val, pred):
    squared_error = np.square(true_val - pred) 
    sum_squared_error = np.sum(squared_error)
    mse_loss = sum_squared_error / true.size
    
    return mse_loss

In machine learning, we aim to lower the MSE value to increase the accuracy of the model.

Mean Absolute Error

The mean absolute error (MAE) measures the amount of error in machine learning models by calculating the total absolute difference between the actual value and the predicted value in our data. This error is also known as L1 loss.

This mean absolute error loss function is more robust to the outliers in comparison with the MSE loss function. Therefore, we can use this loss function when the dataset is prone to too many outliers.

If we have data point Yi and the corresponding predicted value for this data point is Ŷi, then the mean absolute error can be calculated as:

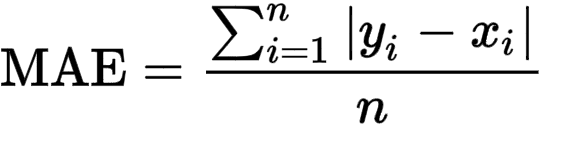
Where n is the total number of observations in our dataset.

Example:

from sklearn.metrics import mean_absolute_error#sample data
actual = [2, 3, 5, 5, 9]
predicted = [3, 3, 8, 7, 6]#calculate MAEerror = mean_absolute_error(actual, predicted)
print(error)

Struggling to track and reproduce complex experiment parameters? Artifacts are just one of the many tools in the Comet toolbox to help ease model management. Read our PetCam scenario to learn more.

Mean Absolute Percentage Error

The mean absolute percentage error (MAPE) loss function measures the amount of error by taking the absolute difference between the actual value and the predicted value in our data and then dividing it by the actual value. We apply the absolute percentage to this value and then average it across our dataset.

This loss function measures the error better than the MSE as it does not penalize large errors. This loss function is commonly used as it normalizes all the errors on a common scale and is easy to interpret.

If we have data point Yi and the corresponding predicted value for this data point is Ŷi, then the mean absolute percentage error can be calculated as:

Where n is the total number of observations in our dataset.

Example:

import numpy as npdef mean_absolute_percentage_error(actual_value, pred):
    abs_error = (np.abs(actual_value - pred)) / actual_value
    sum_abs_error = np.sum(abs_error)
    mape_loss_perc = (sum_abs_error / true.size) * 100    return mape_loss_perc

The smaller the value of MAPE, the better will be the accuracy of the model.

Mean Squared Logarithmic Error

The mean squared logarithmic error (MSLE) measures the amount of error in the machine learning models by taking the ratio between the actual value and the predicted value in our data.

As the name suggests, this loss function is a variation of mean squared error (MSE). We use this loss function when we do not want to significantly penalize the model (as mean squared error) for large errors than the smaller errors.

If we have data point Yi and the corresponding predicted value for this data point is Ŷi, then the mean absolute logarithmic error can be calculated as:

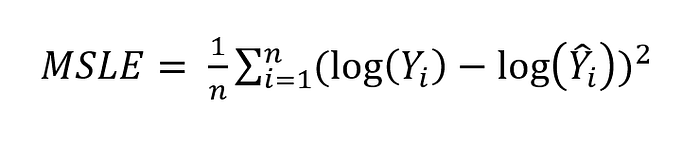
Where n is the total number of observations in our dataset.

Example:

from sklearn.metrics import mean_squared_log_error#sample data
actual = [3, 5, 2.5, 7, 11]
predicted = [2.5, 5, 4, 8, 10.5]#calculate MSLEerror = mean_squared_log_error(actual, predicted)
print(error)

Loss functions for Classification

Binary Cross-Entropy Loss

This binary cross-entropy loss is a default loss function for binary classifiers in machine learning algorithms. It measures the performance of a classification model by comparing the value of each predicted probability with the actual class output such as 0 or 1.

If the difference between the predicted probability and the value of actual class output increases, then the cross-entropy loss increases as well.

Suppose a classifier predicts a probability of 0.09 and the actual observation class is 1, then it would result in a high cross-entropy loss value. The value of this loss function for a model should be closer to 0 ideally, to achieve high accuracy.

Here’s the formula for the cross-entropy loss function:

Here, hθ(xi) is the probability of class 1 and (1-hθ(xi)) is the probability of class 0.

Example:

def binary_cross_entropy(actual, predicted):
	sum_score = 0.0
	for i in range(len(actual)):
		sum_score += actual[i] * log(1e-15 + predicted[i])
	mean_sum_score = 1.0 / len(actual) * sum_score	return -mean_sum_score

Hinge Loss

The hinge loss is an alternative to the cross-entropy loss function. It was initially developed for the performance evaluation of the support vector machine (SVM) algorithm to calculate the maximum margin from the hyperplane to the labelled class.

It is used with binary classification where the target values fall in the range of -1 to 1. This loss function penalizes the wrong predictions by assigning more errors when there is more difference between the actual and predicted value class.

Here’s the formula for the hinge loss function:

Where Sj is the actual value and Syi is the predicted value.

Example:

import numpy as npdef hinge_loss(y, y_pred):
    l = 0
    size = np.size(y)
    for i in range(size):
        l = l + max(0, 1 - y[i] * y_pred[i])    return l / size

Conclusion

That’s all from this article. In this article, we learned about various loss functions in machine learning that are used with regression and classification problems. To achieve better outcomes, it is important to choose the loss function that is the best fitting for our data.

Thanks for reading!