Artificial intelligence (AI) is a buzzword you see pretty much everywhere around you, even when you’re not looking. It has completely dominated tech media, newsrooms, and is even credited with the success of many modern applications.

But does it really work, or is it just hype? Truth is, it does. While there might be some hype around its capabilities, AI has been demonstrated both in research and industry to work really well for a variety of tasks and use cases.

There exist many techniques to make computers learn intelligently, but neural networks are one of the most popular and effective methods, most notably in complex tasks like image recognition, language translation, audio transcription, and so on.

In this two-part series, I’ll walk you through building a neural network from scratch. While you won’t be building one from scratch in a real-world setting, it is advisable to work through this process at least once in your lifetime as an AI engineer. This can really help you better understand how neural networks work.

In this first article, you’ll learn:

—What Artificial Intelligence is

—What Deep Learning is

—What a Neural Network Entails

—Why Neural Networks are Popular

—Build a Neural Network From Scratch

• Why use Python for AI?
• Understanding the Problem
• The Layers of a Neural Network
• The Weights and Biases
• The Activation Function
• The Loss Function
• Going Forward: Forward Propagation
• A Step Backward: Backpropagation
• Optimization and Training of the Neural Network
• Making Predictions
• Putting It All Together

And once you’ve had a chance to work through this tutorial, head on over to part 2, where we actually train and test the network we build.

What Is AI

Artificial intelligence (AI) is an umbrella term used to describe the intelligence shown by machines (computers), including their ability to mimic humans in areas such as learning and problem-solving. This means with AI, you can automate how you think, reason, and make decisions. As such, you can teach a computer to do what humans do, without explicitly programming it.

Despite this simple explanation above, this isn’t as easy as it sounds. And while many scientists and researchers have been able to teach machines to act like humans in areas like computer vision and natural language processing, there’s still serious work to be done before we can have efficient and fully functioning AI systems.

I’m guessing that’s the reason you’re here-to learn how neural networks and AI work in general, and how you can use them to automate your own processes, build customized user experiences, and more.

AI is broad and has numerous subfields, of which machine learning is a part. Machine learning itself has numerous techniques, of which neural networks are one (albeit a very successful technique).

What Is Deep Learning

Deep learning–a machine learning technique–is an efficient way of learning that relies on big data, where features that can help a machine map an input to an output is automatically extracted from layers of “neurons”.

Deep learning is the main technology behind:

• Driverless cars
• Large-scale recommendation engines like Spotify, YouTube, and Amazon
• Language translation services like Google Translate
• Chatbots like Siri and Google assistant.

A neural network is a type of deep learning architecture, and it’s our primary focus in this tutorial. Some specific architectures for deep neural networks include convolutional neural networks (CNN) for computer vision use cases, recurrent neural networks (RNN) for language and time series modeling, and others like generative adversarial networks (GANs) for generative computer vision use cases.

The future of machine learning is on the edge. Subscribe to the Fritz AI Newsletter to discover the possibilities and benefits of embedding ML models inside mobile apps.

What Is a Neural Network

Neural networks are composed of simple building blocks called neurons. While many people try to draw correlations between a neural network neuron and biological neurons, I will simply state the obvious here: “A neuron is a mathematical function that takes data as input, performs a transformation on them, and produces an output”.

This means that neurons can represent any mathematical function; however, in neural networks, we typically use non-linear functions.

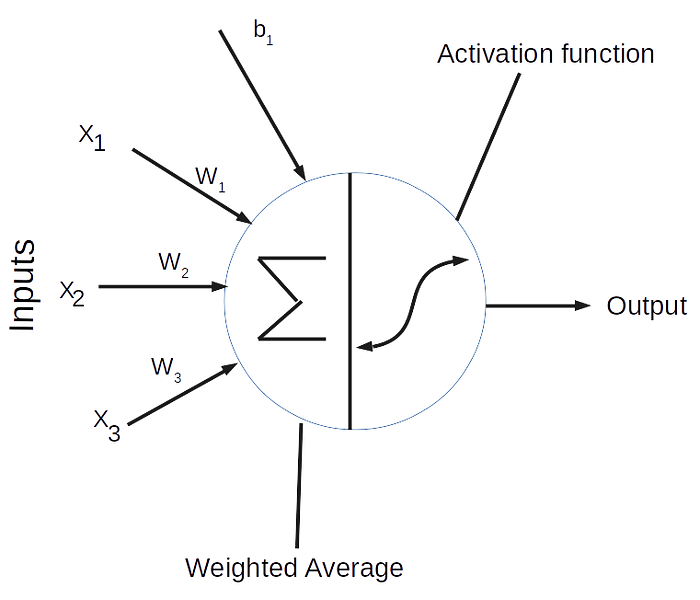
Looking at the neuron above, you can see that it’s composed of two main parts: the summation and the activation function. A neuron takes data (x₁, x₂, x₃) as input, multiplies each with a specific weight (w₁, w₂, w₃), and then passes the result to a nonlinear function called the activation function to produce an output.

A neural network combines multiple neurons by stacking them vertically/horizontally to create a network of neurons-hence the name “neural network”. A simple one-neuron network is called a perceptron and is the simplest network ever.

Another important concept I’ll explain in later sections of this tutorial is how a neural network actually learns the weights it assigns to each input feature. In neural nets, the weights are everything. If you know the correct weight, you can easily output correct predictions.

In summary, what machine learning and deep learning really boils down to is actually trying to find the right weights that generalize to any input.

Why Are Neural Networks Popular?

In the previous section, I introduced neural networks and briefly explained the building blocks. Now we’ll explore why neural networks are popular today.

Neural networks have been around for a really long time—a few major problems with them, and reasons, why people didn’t use them before now, was due to the fact that:

1. They were notoriously difficult to train, in the sense that it can be difficult to get the right weights that generalize to new inputs.
2. They need huge amounts of data.
3. Computing power was still low and expensive.

When these barriers were overcome, neural nets became cool again, and numerous applications sprung up.

Neural networks are also very popular now because of their effectiveness on a wide range of tasks. They can automatically extract features from unstructured data like texts, images, and sounds, and deep learning has greatly reduced the time spent to manually create features.

To illustrate this, I’ll tell you a short story about Google Translate. In the early days of Google Translate, thousands of engineers, language experts, and computer scientists had to work all day to manually extract and create features from texts.

These manual features had to be fed into machine learning models. Even with this time consuming and expensive task, the performance of these systems was nothing close to human-like. But when Geoff Hilton’s team showed that a neural network could be trained using a technique called backpropagation, Google switched from manually engineering features to using deep neural nets, and this greatly improved performance.

This anecdote shows that with enough data and compute power, neural networks can do better than other machine learning algorithms—hence, their rising popularity.

Building a Neural Network From Scratch

Now that you’ve gotten a brief introduction to AI, deep learning, and neural networks, including some reasons why they work well, you’re going to build your very own neural net from scratch. To do this, you’ll use Python and its efficient scientific library Numpy.

Why Python for AI?

Python is a high-level, interpreted, and general-purpose language that can be used for a wide variety of tasks. It’s one of the easiest languages to learn, and that makes it the go-to for new programmers. Python is popular among AI engineers—in fact, the majority of AI applications are built with Python and Python-related tools. There are many reasons for this, some of which include:

1. There is a large ecosystem of pre-built libraries for scientific computation. Libraries like NumPy, SciPy, and Pandas make doing scientific calculations easy and quick, as the majority of these libraries are well-optimized for common ML and DL tasks.
2. Python is platform-independent and can be run on almost all devices. This means Python is easily compatible across platforms and can be deployed almost anywhere.
3. Python has a helpful and supportive community built around it, and this community provides tons of guides and tutorials for working with the language. You can rest assured that most problems you encounter have already been solved.

I love the comic below that shows a flying programmer *winks. It depicts why Python is easy to learn, with numerous libraries that you can import and use for almost any task—including antigravity 😂!

Before you start flying, it is essential you’ve properly set up your machine learning environment. If not, you should visit this page first before moving onto the next section.

What Are You Trying to Solve?

Before you start writing code, let’s talk about the problem you’re going to solve, as a more complete understanding of the problem will help you form the solution. In this tutorial, you’re are going to create a neural network that predicts if a person will have heart disease or not. You’ll use a heart disease dataset from the UCL data repository. You can download it here.

On the dataset page, click on Data Folder and download the heart.dat file. This comes in a .dat file format. Create a new directory where your Jupyter Notebook and Data will live. Then, copy the heart.dat file to the folder.

Next, you can create a new notebook and add the following lines of code:

#prepare data downloaded from UCL

import csv
import pandas as pd

# add header names
headers =  ['age', 'sex','chest_pain','resting_blood_pressure',  
        'serum_cholestoral', 'fasting_blood_sugar', 'resting_ecg_results',
        'max_heart_rate_achieved', 'exercise_induced_angina', 'oldpeak',"slope of the peak",
        'num_of_major_vessels','thal', 'heart_disease']

heart_df = pd.read_csv('heart.dat', sep=' ', names=headers)

In the code block above, you first set the header, which is the column names for the data set. You can get these names from the dataset description file also in the data page. Notice the sep parameters passed to Pandas read function? this tells pandas that the data is separated by spaces and not the default commas.

In the next code block, you’ll print out the head of the data:

heart_df.head()

From the head of the data, you can see the features present, and you can begin to imagine the kind of analysis you’ll need to perform on the dataset. Next, print out the shape of the data:

heart_df.shape

(270, 14)

There are 270 observations. This means that your neural network will have an input data of shape 270 x 13, excluding the target variable (heart_disease). The features present in the dataset are:

• age
• sex
• chest pain type (4 values)
• resting blood pressure
• serum cholesterol in mg/dl
• fasting blood sugar > 120 mg/dl
• resting electrocardiographic results (values 0,1,2)
• maximum heart rate achieved
• exercise-induced angina
• oldpeak (ST depression induced by exercise relative to rest)
• the slope of the peak exercise ST segment
• number of major vessels (0–3) colored by fluoroscopy
• thal (3 = normal; 6 = fixed defect; 7 = reversible defect)
• heart_disease: absence (1) or presence (2) of heart disease

Next, you can check for missing values and also the data types. A Neural Network expects all features to be numeric and not contain missing values.

heart_df.isna().sum()

heart_df.dtypes

There are no missing values in the dataset, and all features are numeric. Next, you’ll separate the target from the data, split into train and test set, and then standardize the data.

import numpy as np
import warnings
warnings.filterwarnings("ignore") #suppress warnings
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

#convert imput to numpy arrays
X = heart_df.drop(columns=['heart_disease'])

#replace target class with 0 and 1 
#1 means "have heart disease" and 0 means "do not have heart disease"
heart_df['heart_disease'] = heart_df['heart_disease'].replace(1, 0)
heart_df['heart_disease'] = heart_df['heart_disease'].replace(2, 1)

y_label = heart_df['heart_disease'].values.reshape(X.shape[0], 1)

#split data into train and test set
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y_label, test_size=0.2, random_state=2)

#standardize the dataset
sc = StandardScaler()
sc.fit(Xtrain)
Xtrain = sc.transform(Xtrain)
Xtest = sc.transform(Xtest)

print(f"Shape of train set is {Xtrain.shape}")
print(f"Shape of test set is {Xtest.shape}")
print(f"Shape of train label is {ytrain.shape}")
print(f"Shape of test labels is {ytest.shape}")

In the code block above, first, you dropped the target from the training dataset, and the replace the classes with 0 and 1. Notice you reshaped the y_label to a 1-D array. This is important when you start performing dot products. Next, you used the handy train_test_split function from sklearn to split the data into train and test set, with the test set taking 20 percent of the data. Finally, you standardized the dataset using the StandardScaler module of sklearn.

The Layers of a Neural Network

Now that you have downloaded and prepared the dataset, let’s start building the neural network to make predictions. To do that, you first, need to understand the concept of layers.

Remember when I said a neural network stacks multiple neurons together to build really large and complex mathematical functions? Well, the official name for it is a layer. The layer is a collection of nodes at different stages of computation in a neural network. Each node acts as a neuron and performs calculations on the data passed to it. Look at the illustration of a 3-layer neural network below:

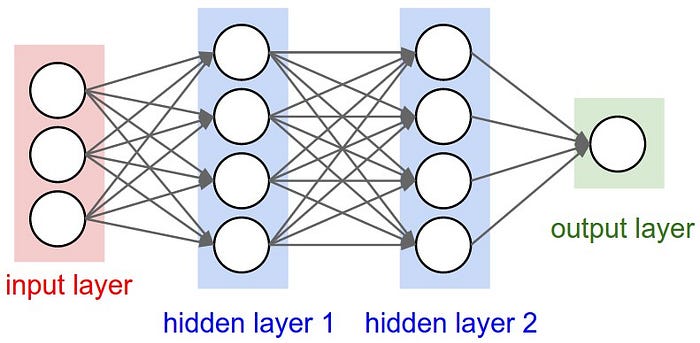
Yeah I know, you see four layers—but in deep learning, you don’t count the first layer. The first layer is called the input layer, and the number of nodes will depend on the number of features present in your dataset. In our case, it will be 13 nodes because we have 13 features.

The final layer of the neural network is called the output layer, and the number depends on what you’re trying to predict. For regression and binary classification tasks, you can use a single node; while for multi-class problems, you’ll use multiple nodes, depending on the number of classes.

In this article, you’ll use a single node for your final layer, because you’re working on a binary classification task.

The layers between the input and the final layer is where the magic happens— these are called the hidden layers. The hidden layers can be as deep or wide as you want, and while a deeper network is better, the computational time also increases as you go deeper.

In order to keep things relatively simple, you’re going to design and code a 2-layer neural network. Below is a preview of the architecture:

The neural net above will have one hidden layer and a final output layer. The input layer will have 13 nodes because we have 13 features, excluding the target. The hidden layer can accept any number of nodes, but you’ll start with 8, and the final layer, which makes the predictions, will have 1 node. Next, let’s talk about weights and biases that each layer must-have.

The Weights and Biases

Weights and biases are the learnable parameters that help a neural network correctly learn a function. Think of weights as a measure of how sure you are that a feature contributes to a prediction and the bias as a base value that your predictions must start from.

I’ll give you an illustration.

Assume you’re a machine learning model, and you want to predict if a person is rich or not, and you have been given the following clues to help you make that decision:

• Age of the person
• Height of the person
• Salary of the person

The clues above are what we call features in machine learning, and what you want to predict is called the target/label/ground truth. The label can be one of two classes (rich, not rich)—in other words, binary classification.

Basically, what you want to do is combine the features in such a way that they help you more accurately predict the outcome.

y(rich, not rich) = Age + Height + salary + [base]

Assuming we set a base salary of $3000, and Person 1 has the following features; age = 18, height = 5.6ft, salary = $2000, then you’ll calculate the richness as follows:

y(rich, not rich) = 18 + 5.6 + 2000 + 3000 = ~5024

For this example, we might define a threshold for richness as any value greater than $40,000. Judging by these criteria, you can conclude that person 1 is not rich. Let’s look at another example.

Person 2 has the following features; age = 26, height = 5.2ft and salary = $50,000. Your prediction will calculated as:

y(rich, not rich) = 26 + 5.2 + 50000 + 3000 = ~53031

Then, by the threshold earlier stated, person 2 is rich.

It’s obvious that some clues are more important than others. Can you guess which one is the most important? Yes! Salary. This is, perhaps unsurprisingly, an important factor that indicates whether a person is rich or not.

Using this idea, you can assign importance to the features. For instance, you can assign weights as follows:

y(rich,not rich) = (2 * Age) + (1 * Height) + (8 * Salary) + base

Intuitively, we assign a higher value to the salary feature.

The importance of the value can be any number but must be representative of scale.

You might be wondering what the base value of 3000 is and why we add it to the predictions. This value is called the bias. It is a base value that every prediction must-have, even when nothing else is given.

Now, if you make a prediction for person 1 and 2 again, you’ll have the following:

Person 1: (2 * 18) + (1 * 5.6) (8 * 2000) + 3000 = ~19041 (still poor)

Person 2: (2 * 26) + (1 * 5.2) + (8 * 5000) + 3000 = ~43057 (Still rich)

What if a person has no value for age, height, and salary, then your prediction will be?

y(rich, not rich) = (2 * 0) + (1 * 0) (8 * 0) + 3000 = 3000

Now you see where the bias value comes in.

What you should take away from the examples above is the fact that importance values assigned to features are called weights, and the base value is called the bias.

A machine learning model uses lots of examples to learn the correct weights and bias to assign to each feature in a dataset to help it correctly predict outputs.

Back to our proposed solution. You now know that every feature in our dataset must be assigned a weight and that after doing a weighted sum, you add a bias term.

In the code block below, you’ll create your neural network class and initialize those weights and biases:

class NeuralNet():
    '''
    A two layer neural network
    '''
        
    def __init__(self, layers=[13,8,1], learning_rate=0.001, iterations=100):
        self.params = {}
        self.learning_rate = learning_rate
        self.iterations = iterations
        self.loss = []
        self.sample_size = None
        self.layers = layers
        self.X = None
        self.y = None
                
    def init_weights(self):
        '''
        Initialize the weights from a random normal distribution
        '''
        np.random.seed(1) # Seed the random number generator
        self.params["W1"] = np.random.randn(self.layers[0], self.layers[1]) 
        self.params['b1']  =np.random.randn(self.layers[1],)
        self.params['W2'] = np.random.randn(self.layers[1],self.layers[2]) 
        self.params['b2'] = np.random.randn(self.layers[2],)

First, you create a neural network class, and then during initialization, you created some variables to hold intermediate calculations. The argument layers is a list that stores your network’s architecture. You can see that it accepts 13 input features, uses 8 nodes in the hidden layer (as we noted earlier), and finally uses 1 node in the output layer. We’ll talk about the other parameters such as the learning rate, sample size and iterations in later sections.

Moving on to the next code section, you created a function (init_weights) to initialize the weights and biases as random numbers. These weights are initialized from a uniform random distribution and saved to a dictionary called params.

You’ll notice that there are two weight and bias arrays. The first weight array (W1) will have dimensions of 13 by 8—this is because you have 13 input features and 8 hidden nodes, while the first bias (b1) will be a vector of size 8 because you have 8 hidden nodes.

The second weight array (W2) will be a 10 by 1-dimensional array because you have 10 hidden nodes and 1 output node, and finally, the second bias (b2) will be a vector of size because you have just 1 output.

I’m guessing you’re seeing a pattern here. That is, if you have a neural network with the following architecture [20,30,2], then you know you’ll have the following dimensions for your weights and biases:

W1 = (20,30) , b1 = (30,)

W2 = (30, 2), b2 = (2,)

And if you have a 3 layer architecture like [5,7,8,2], then you know you’ll have 3 weights and 3 biases with the following shapes:

W1 = (5,7), b1 = (7,)

W2 = (7,8), b2 = (8,)

W3 = (8,2), b3 = (2,)

So what will the dimensions be for a neural network with this architecture [20, 23, 2]?

The Activation Function

Now that you’ve initialized the weights and biases, let’s talk about activation functions. Activations are the nonlinear computations done in each node of a Neural Network. Remember when I told you that each node performs some mathematical computation? Well, that computation happens in two phases.

First, you do a weighted sum of the input and the weights, add the biases, and then pass the result through an activation function. I’ll explain why we do that below.

An activation function is what makes a neural network capable of learning complex non-linear functions. Non-linear functions are difficult for traditional machine learning algorithms like logistic and linear regression to learn. The activation function is what makes a neural network capable of understanding these functions.

There are many types of activation functions used in deep learning—some popular ones are Sigmoid, ReLU, tanh, Leaky ReLU, and so on. Each activation function has its pros and cons, but the ReLU function has been shown to perform very well, so in this article, you’ll use the ReLU function.

The activation function is computed by each node in the hidden layers of a neural network. This means you’ll have to pass the weighted sums through the ReLU function.

But what is ReLU?

ReLU (Rectified Linear Unit) is a simple function that compares a value with zero. That is, it will return the value passed to it if it is greater than zero; otherwise, it returns zero.

The code for the ReLU function is shown below:

def relu(self,Z):
        '''
        The ReLu activation function is to performs a threshold
        operation to each input element where values less 
        than zero are set to zero.
        '''
        return np.maximum(0,Z)

You’ll add this inside the NeuralNetwork class. This function performs an array-wise ReLU because you’ll be dealing mainly with arrays, not single values.

In summary, the hidden layer receives values from the input layer, calculates a weighted sum, adds the bias term, and then passes each result through an activation function—in our case a ReLU. The result from the ReLU is then passed to the output layer, where another weighted sum is performed using the second weights and biases. But then instead of passing the result through another activation function, it is passed through what I like to call the output function.

The output function will depend on what you’re trying to predict. You can use a sigmoid function when you have a two-class problem (binary classification), and you can use a function called softmax for multi-class problems.

In this tutorial, you’ll be using a sigmoid function for the output layer. This is because you’re predicting one of two classes.

The sigmoid function takes a real number and squashes it to a value between 0 and 1. In other words, it outputs a probability score for every real number. This is useful for the task at hand because you don’t just want your model to predict a yes (1) or No (0)—you want it to predict probabilities that can help you measure how sure it is of its predictions.

Let’s add the Sigmoid function to our NeuralNetwork class:

def sigmoid(self,Z):
        '''
        The sigmoid function takes in real numbers in any range and 
        squashes it to a real-valued output between 0 and 1.
        '''
        return 1/(1+np.exp(-Z))

You’ll use the Numpy exponential function to code the sigmoid function. This makes it possible to perform the operation for arrays instead of single values. Also, Numpy implementation is faster than pure Python, as it’s written in C.

The Loss Function

Next, let’s talk about a neural network’s loss function. The loss function is a way of measuring how good a model’s prediction is so that it can adjust the weights and biases.

A loss function must be properly designed so that it can correctly penalize a model that is wrong and reward a model that is right. This means that you want the loss to tell you if a prediction made is far or close to the true prediction. The choice of the loss function is dependent on the task—and for classification problems, you can use cross-entropy loss.

Where C is the number of classes, y is the true value and y_hat is the predicted value.

For a binary classification task (i.e. C=2), the cross-entropy loss function becomes:

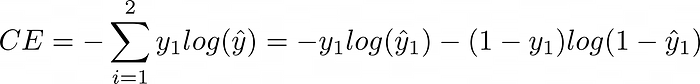
Now, let’s put this in code:

Update (05–02–2021):

The loss function below has been updated to take into consideration 0 values. If our NN supplies 0 values to log, it will result in infinity, which will affect network training. So here, we compare the value, and if it is zero, we replace with an extremely small value (0.00000001)

def eta(self, x):
  ETA = 0.0000000001
  return np.maximum(x, ETA)

def entropy_loss(self,y, yhat):
    nsample = len(y)
    yhat_inv = 1.0 - yhat
    y_inv = 1.0 - y
    yhat = self.eta(yhat) ## clips value to avoid NaNs in log
    yhat_inv = self.eta(yhat_inv) 
    loss = -1/nsample * (np.sum(np.multiply(np.log(yhat), y) + np.multiply((y_inv), np.log(yhat_inv))))
    return loss

Notice the sum and the division by sample size in the code block above? This means you’re considering the average loss with respect to all the inputs. That is, you’re concerned about the combined loss from all the samples and not the individual losses.

Going Forward: Forward Propagation

Now that you have some basic building blocks for your neural network, you’ll move to a very important part of the process called forward propagation.

Forward propagation is the name given to the series of computations performed by the neural network before a prediction is made. In your two-layer network, you’ll perform the following computation for forward propagation:

• Compute the weighted sum between the input and the first layer’s weights and then add the bias: Z1 = (W1 * X) + b
• Pass the result through the ReLU activation function: A1 = Relu(Z1)
• Compute the weighted sum between the output (A1) of the previous step and the second layer’s weights—also add the bias: Z2 = (W2 * A1) + b2
• Compute the output function by passing the result through a sigmoid function: A2 = sigmoid(Z2)
• And finally, compute the loss between the predicted output and the true labels: loss(A2, Y)

And there, you have the forward propagation for your two-layer neural network. For a three-layer neural network, you’d have to compute Z3 and A2using W3 and b3 before the output layer.

Now, let’s put this in code. Remember to add the code to your NeuralNetwork class:

    
    def forward_propagation(self):
        '''
        Performs the forward propagation
        '''
        
        Z1 = self.X.dot(self.params['W1']) + self.params['b1']
        A1 = self.relu(Z1)
        Z2 = A1.dot(self.params['W2']) + self.params['b2']
        yhat = self.sigmoid(Z2)
        loss = self.entropy_loss(self.y,yhat)

        # save calculated parameters     
        self.params['Z1'] = Z1
        self.params['Z2'] = Z2
        self.params['A1'] = A1

        return yhat,loss

In the code cell above, first, you perform all the dot products and addition using the weights and biases you initialized earlier, calculate the loss by calling the entropy_loss function, save the calculated parameters and finally return the predicted values and the loss. These values will be used during backpropagation.

Wheeew! That’s a lot to take in, I’m happy to inform you that you’re halfway to the completion of your neural net. Take a moment to smile!

A Step Backward: Backpropagation

Backpropagation is the name given to the process of training a neural network by updating its weights and bias.

A neural network learns to predict the correct values by continuously trying different values for the weights and then comparing the losses. If the loss function decreases, then the current weight is better than the previous, or vice versa. This means that the neural net has to go through many training (forward propagation) and update (backpropagation) cycles in order to get the best weights and biases. This cycle is what we generally refer to as the training phase, and the process of searching for the right weights is called optimization.

Now the question is, how do you code a neural network to correctly adjust its weights with respect to the loss it calculates. Well, thanks to mathematics, we can use calculus to do this effectively. So the calculus you learnt in school is important after all 😉.

A Primer on Calculus

Calculus helps us understand how a change in one variable affects another variable. That is, you can use calculus to compute how much changing the weights/bias affects the loss function. So basically, we use calculus to understand how much and in what direction to update weights and bias in order to decrease the loss.

Assume you have a function y = x². This function is telling you that the value of y is 2 times the value of x. i.e. if x = 2, then y = 4, if x = 4, then y = 16.

Now using calculus, you can calculate the relationship between y and x. We call this the derivative of y with respect to x.

You can easily know the rate of change of many functions through special calculated derivatives. These derivatives are formulas that have been studied and can quickly be used to calculate complex derivatives. For instance, in the function y = x², the derivative is 2x. This means the rate of change is 2 times the value of x. Now how was this calculated? According to calculus, you can calculate the derivative of a function of the form y = xⁿ using the formula:

For example, if y = X⁴, then n=4, so the derivative will be calculated as:

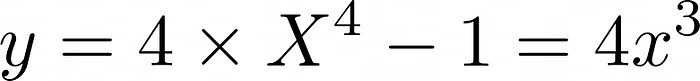
What if you have special functions like sigmoid, ReLU, tanh, Sin, or a combination of multiple functions like 3x + 2x²—how do you calculate the derivative? The good news is that most of these functions are built from a combination of smaller functions, so you can use a concept of chaining to aggregate the derivatives—enter the chain rule!

So if you have two functions that are dependent on each other—say 2x² + 3x— then the derivative becomes the addition of the individual derivatives:

But if two functions are multiplied, the computation differs. Here’s an instance—assuming you need to find the derivative of this function y = 2x⁴ × 4x², you can calculate the derivative as follows:

First, assign an alphabet to each function; so let’s say a is assigned the first part, i.e. a = 2x⁴ and b is assigned the second part, i.e. b = 4x². Then the derivative becomes:

This means that for two functions multiplied together, you first take the derivative of the first part a (Δa), and multiply it with the second part b, then take the derivative of the second part b (Δb), and multiply it with the first part a, and finally, you sum the result. So, therefore, the derivative becomes:

and from laws of indices, this reduces to:

Now, I don’t plan to show you all the derivatives available in calculus, but basically, you should know that most derivatives you’ll be using while coding the backpropagation algorithm have already been computed, so you can just use the formulas.

A couple of great resources to learn more about derivatives here:

Using Calculus in Backpropagation

After computing the output and loss in the forward propagation layer, you’ll move to the backpropagation phase, where you calculate the derivatives backward, from the loss all the way up to the first weight and bias. To perform backpropagation in your neural network, you’ll follow the steps listed below:

Starting from the last layer, calculate the derivative of the loss with respect to the output yhat as:

But how did you get to the loss? Well, you calculated the sigmoid(Z2). Now, what is the derivative of the loss with respect to the sigmoid(Z2)?

Sigmoid(Z2) is a combination of two functions, so you have to calculate two derivatives:

First, calculate the derivative of sigmoid activation with respect to (wrt) the loss:

Then, you calculate the derivative of the loss wrt Z2:

Now, how did you get Z2? You calculated a dot product between A1 and W2, and added a bias b2. This means that you have to calculate the loss with respect to all these variables:

And how did you get to A1? You performed ReLU(Z1). So you take the derivative of ReLU and Z1 wrt to the loss as well. The derivative of ReLU is 1 if the input is greater than 1, and 0 otherwise.

You’ll create a function to compute this and call it dRelu:

Next, how did you get Z1? You computed the dot product between X and W1and added the bias b1. So you compute the derivative of all the variables involved, except the input X.

Note: dl_wrt is read “the loss with respect to”

Pheeewww! You now have all your derivatives for the backpropagation algorithm. If you want a detailed overview of how these derivatives are calculated from scratch, this Medium post is a great guide.

Next, let’s write the backpropagation code:

def back_propagation(self,yhat):
        '''
        Computes the derivatives and update weights and bias according.
        '''
        y_inv = 1 - self.y
        yhat_inv = 1 - yhat

        dl_wrt_yhat = np.divide(y_inv, self.eta(yhat_inv)) - np.divide(self.y, self.eta(yhat))
        dl_wrt_sig = yhat * (yhat_inv)
        dl_wrt_z2 = dl_wrt_yhat * dl_wrt_sig

        dl_wrt_A1 = dl_wrt_z2.dot(self.params['W2'].T)
        dl_wrt_w2 = self.params['A1'].T.dot(dl_wrt_z2)
        dl_wrt_b2 = np.sum(dl_wrt_z2, axis=0, keepdims=True)

        dl_wrt_z1 = dl_wrt_A1 * self.dRelu(self.params['Z1'])
        dl_wrt_w1 = self.X.T.dot(dl_wrt_z1)
        dl_wrt_b1 = np.sum(dl_wrt_z1, axis=0, keepdims=True)

In the backpropagation function, first, you create a function to calculate the derivatives of the ReLU, then you calculate and save the derivative of every parameter with respect to the loss function.

Notice we use a common naming scheme (dl_wrt). This helps keep your code clean and easy to read. Once you calculate these derivatives, you have to update your previous weights. That is the essence of computing derivatives—you basically want to know how to update your weights in order to minimize the loss.

Optimization and Training of the Neural Network

In the previous section, you used calculus to compute the derivatives of the weights and biases with respect to the loss. The model now knows how to change them. To automatically use this information to update the weights and biases, a neural network must perform hundreds, thousands, and even millions of forward and backward propagations. That is, in the training phase, the neural network must perform the following:

• Forward propagation
• Backpropagation
• Weight updates with calculated gradients
• Repeat

Let’s write the code that updates the weights and biases. In your backpropagation function, add the following lines of codes:

#update the weights and bias
self.params['W1'] = self.params['W1'] - self.learning_rate * dl_wrt_w1
self.params['W2'] = self.params['W2'] - self.learning_rate * dl_wrt_w2
self.params['b1'] = self.params['b1'] - self.learning_rate * dl_wrt_b1
self.params['b2'] = self.params['b2'] - self.learning_rate * dl_wrt_b2

What you’re basically doing here is subtracting the derivative multiplied by a small value called the learning rate. The learning rate is a value that tells our neural network how big the update should be.

Now that you’ve added the lines of code to perform the updates, you’ll create a new function called fit that takes the input (X) and labels (Y) and calls the forward and backpropagation repeatedly for a specified number of iterations:

def fit(self, X, y):
        '''
        Trains the neural network using the specified data and labels
        '''
        self.X = X
        self.y = y
        self.init_weights() #initialize weights and bias


        for i in range(self.iterations):
            yhat, loss = self.forward_propagation()
            self.back_propagation(yhat)
            self.loss.append(loss)

The fit function takes 2 parameters: X(input dataset) and y (labels). First, it saves the train and target to the class variable and then initializes the weights and biases by calling the init_weights function. Then, it loops through the specified number of iterations, performs forward and backpropagation, saves the loss.

Making Predictions

To make predictions, you simply make a forward pass on the test data. That is, you use the saved weights and biases from the training phase. To make the process easier, you’ll add a function to your NeuralNetwork class called predict:

def predict(self, X):
        '''
        Predicts on a test data
        '''
        Z1 = X.dot(self.params['W1']) + self.params['b1']
        A1 = self.relu(Z1)
        Z2 = A1.dot(self.params['W2']) + self.params['b2']
        pred = self.sigmoid(Z2)
        return np.round(pred)

The function passes the data through the forward propagation layer and computes the prediction using the saved weights and biases. The predictions are probability values ranging from 0 to 1. In order to interpret these probabilities, you can either round up the values or use a threshold function. To keep things simple, we just rounded up the probabilities.

Putting It Together

Let’s put all your code together:

class NeuralNet():
    '''
    A two layer neural network
    '''
        
    def __init__(self, layers=[13,8,1], learning_rate=0.001, iterations=100):
        self.params = {}
        self.learning_rate = learning_rate
        self.iterations = iterations
        self.loss = []
        self.sample_size = None
        self.layers = layers
        self.X = None
        self.y = None
                
    def init_weights(self):
        '''
        Initialize the weights from a random normal distribution
        '''
        np.random.seed(1) # Seed the random number generator
        self.params["W1"] = np.random.randn(self.layers[0], self.layers[1]) 
        self.params['b1']  =np.random.randn(self.layers[1],)
        self.params['W2'] = np.random.randn(self.layers[1],self.layers[2]) 
        self.params['b2'] = np.random.randn(self.layers[2],)
    
    def relu(self,Z):
        '''
        The ReLu activation function is to performs a threshold
        operation to each input element where values less 
        than zero are set to zero.
        '''
        return np.maximum(0,Z)

    def dRelu(self, x):
        x[x<=0] = 0
        x[x>0] = 1
        return x

    def eta(self, x):
      ETA = 0.0000000001
      return np.maximum(x, ETA)


    def sigmoid(self,Z):
        '''
        The sigmoid function takes in real numbers in any range and 
        squashes it to a real-valued output between 0 and 1.
        '''
        return 1/(1+np.exp(-Z))

    def entropy_loss(self,y, yhat):
        nsample = len(y)
        yhat_inv = 1.0 - yhat
        y_inv = 1.0 - y
        yhat = self.eta(yhat) ## clips value to avoid NaNs in log
        yhat_inv = self.eta(yhat_inv) 
        loss = -1/nsample * (np.sum(np.multiply(np.log(yhat), y) + np.multiply((y_inv), np.log(yhat_inv))))
        return loss

    def forward_propagation(self):
        '''
        Performs the forward propagation
        '''
        
        Z1 = self.X.dot(self.params['W1']) + self.params['b1']
        A1 = self.relu(Z1)
        Z2 = A1.dot(self.params['W2']) + self.params['b2']
        yhat = self.sigmoid(Z2)
        loss = self.entropy_loss(self.y,yhat)

        # save calculated parameters     
        self.params['Z1'] = Z1
        self.params['Z2'] = Z2
        self.params['A1'] = A1

        return yhat,loss

    def back_propagation(self,yhat):
        '''
        Computes the derivatives and update weights and bias according.
        '''
        y_inv = 1 - self.y
        yhat_inv = 1 - yhat

        dl_wrt_yhat = np.divide(y_inv, self.eta(yhat_inv)) - np.divide(self.y, self.eta(yhat))
        dl_wrt_sig = yhat * (yhat_inv)
        dl_wrt_z2 = dl_wrt_yhat * dl_wrt_sig

        dl_wrt_A1 = dl_wrt_z2.dot(self.params['W2'].T)
        dl_wrt_w2 = self.params['A1'].T.dot(dl_wrt_z2)
        dl_wrt_b2 = np.sum(dl_wrt_z2, axis=0, keepdims=True)

        dl_wrt_z1 = dl_wrt_A1 * self.dRelu(self.params['Z1'])
        dl_wrt_w1 = self.X.T.dot(dl_wrt_z1)
        dl_wrt_b1 = np.sum(dl_wrt_z1, axis=0, keepdims=True)

        #update the weights and bias
        self.params['W1'] = self.params['W1'] - self.learning_rate * dl_wrt_w1
        self.params['W2'] = self.params['W2'] - self.learning_rate * dl_wrt_w2
        self.params['b1'] = self.params['b1'] - self.learning_rate * dl_wrt_b1
        self.params['b2'] = self.params['b2'] - self.learning_rate * dl_wrt_b2

    def fit(self, X, y):
        '''
        Trains the neural network using the specified data and labels
        '''
        self.X = X
        self.y = y
        self.init_weights() #initialize weights and bias


        for i in range(self.iterations):
            yhat, loss = self.forward_propagation()
            self.back_propagation(yhat)
            self.loss.append(loss)

    def predict(self, X):
        '''
        Predicts on a test data
        '''
        Z1 = X.dot(self.params['W1']) + self.params['b1']
        A1 = self.relu(Z1)
        Z2 = A1.dot(self.params['W2']) + self.params['b2']
        pred = self.sigmoid(Z2)
        return np.round(pred) 

    def acc(self, y, yhat):
        '''
        Calculates the accutacy between the predicted valuea and the truth labels
        '''
        acc = int(sum(y == yhat) / len(y) * 100)
        return acc


    def plot_loss(self):
        '''
        Plots the loss curve
        '''
        plt.plot(self.loss)
        plt.xlabel("Iteration")
        plt.ylabel("logloss")
        plt.title("Loss curve for training")
        plt.show()

Congratulations, you now have a fully functional, 2-layer neural network for a binary classification task. You should give yourself a pat on the back. But before proclaiming complete victory, let’s see if your network actually works.

In the next post, you’ll make predictions, and also compare your network’s predictions with popular deep learning libraries.

If you have any questions, suggestions, or feedback, don’t hesitate to use the comment section below.

Connect with me on Twitter.

Connect with me on LinkedIn.